FIA 1500 Astrofísica General 2004-1


Profesor: Alejandro Clocchiatti

Tarea 3 - Fecha de entrega: Mayo 10, 2004

Ejercicio 1

La observación del espectro del Sol, muestra que el mismo emite muy aproximadamente como un cuerpo negro a una temperatura de $\sim$6000 K. Si el sol fuera un cuerpo negro esférico con un radio de $\sim 7 \times 10^5$km y con una temperatura interna uniforme e igual a la de la radiación que emite (es decir, 6000 K), y su único contenido energético fuera la radiación:

¿Cuál sería el tiempo característico $t_0$, transcurrido el cual la hipótesis de que es un cuerpo negro dejaría de ser válida? (Sugerencia: Relacione el número de fotones por unidad de frecuencia que el Sol pierde en un segundo, con el número total de fotones de que dispone en cada frecuencia). ¿Ha existido el sol más que $t_0$?

Ejercicio 2

Refine su cálculo ahora asumiendo que el sol no es un cuerpo negro perfecto, sino que irradia como un cuerpo negro a $\sim$6000 K pero que en realidad su temperatura interna es mayor. A partir de información de modelos estelares sabemos que la temperatura en el centro del sol es aproximadamente $10^7$K. Asuma, burdamente, que la temperatura es una función lineal del radio.

1. Calcule la energía total que tiene el sol en el campo radiativo (llamada $U$ en clase).

2. Calcule $L_\odot$, la luminosidad bolométrica del sol, asumiendo que emite radiación térmica con temperatura efectiva $T_{\rm eff} = 5770\,$K (y el mismo radio que antes). Usando $U$ y $L_\odot$ estime un nuevo valor de $t_0$. ¿Ha existido el sol más que $t_0$?

Ejercicio 3

Refine su cálculo aún más asumiendo que el sol no es un cuerpo negro, sino que es un objeto esféricamente simétrico que emite radiación térmica desde una región con opacidad alta cercana a su superficie, pero que tiene un contenido energético mayor que el que existe en su campo radiativo interno. A partir de información de modelos estelares sabemos que la densidad en el centro del sol es aproximadamente 160 ${\rm g cm^{-3}}$, que (en comparación) la densidad en el borde externo es despreciable (cero), y que en términos de masa está compuesto mayoritariamente por hidrógeno ionizado (implica que hay dos partículas por cada átomo de hidrógeno). Asuma (también burdamente) que la densidad, al igual que la temperatura, es una función lineal del radio y calcule la energía térmica total encerrada en el sol en forma de movimiento translacional de sus particulas ( $1/2 {\rm k \, T}$ por grado de libertad de cada partícula).

Usando la luminosidad obtenida en el ejercicio anterior, estime un nuevo valor para $t_0$, el tiempo característico en que el sol perderá toda esta energía térmica. Considerando que la edad de la Tierra es de $4.6\times 10^9$ años. ¿Ha existido el sol más que $t_0$? Especule sobre las posibles respuestas a este dilema.

Ejercicio 4

¿Que pasaría con el $t_0$ estimado en el ejercicio anterior, si el radio del sol se redujera en un factor 100 (orden de magnitud del tamaño de una estrella enana blanca) sin alterar el contenido calórico del mismo? ¿Podría una estrella así haber existido desde el comienzo del tiempo (edad del Universo $\sim 15\times 10^{9}\,$años)?

Ejercicio 5

En el Ejercicio 7 de la Tarea 1 se le pidió que assumiera que el flujo total emitido por HZ 21 era igual al emitido por el Sol, para estimar la distancia a la misma. Sabiendo que el espectro del Sol está bien representado por un cuerpo negro a $~$6000 K, y el de HZ 21 por el uno a $~$50000 K, calcule cual es la razón entre el flujo superficial de ambas estrellas. ¿Es razonable la hipótesis hecha en la Tarea 1?

Ejercicio 6

Una nube de material interestelar homogenea de longitud $s$ y temperatura $T_{\rm nube}=6000$ K, está compuesta de partículas con densidad $n = 10$cm$^{-3}$, cuya sección eficaz de absorción es $\sigma_\lambda = 1\times 10^{-21}\, Q_\lambda \ \ [{\rm cm}^2]$ con la función adimensional $Q_\lambda$ dada por (ver figura):

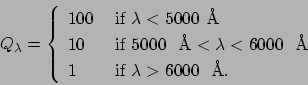$$Q_\lambda = \left\{ \begin{array}{ll} 100 & \mbox{ if $ \la... ...& \mbox{ if $ \lambda > 6000$\ { \AA}}. \\ \end{array}\right.$$ (1)

*.- Calcule la profundidad óptica de la nube para radiación de 4500, 5500 y 6500 Å, para nubes de $s=$2 pc y $s=$80 pc.

Ejercicio 7

La nube anterior se encuentra situada entre un observador y una estrella que emite radiación con intensidad específica $I_\lambda^0$. Asuma $I_\lambda^0 = B_\lambda(T_{\rm star})$, con $B_\lambda(T)$ la función de Plank, y $T_{\rm star}=$10000 K, y que la nube emite radiación térmica con intensidad específica $B_\lambda(T_{\rm nube})$.

*.- ¿Qué temperatura de brillo para la estrella mediría un observador que determinara la intensidad específica con filtros angostos centrados en 4500, 5500 y 6500 Å, para nubes de $s=$2 pc y $s=$80 pc? ¿En que caso podría el observador concluir que está observando un cuerpo negro, y cuál sería su temperatura?

Ejercicio 8

Para un grupo de objetos astronómicos que emiten radiación con intensidad específica dada por la ley de Plank:

$$B_\lambda(T) = {{2 h c^2}\over{\lambda^5}} \left(e^{{h c}\over{\lambda k T}} - 1\right)^{-1}$$

1. Defina el índice de color $I(\lambda_1 , \lambda_2)$ con $\lambda_1 < \lambda_2$, y expréselo como función de $\lambda_1$, $\lambda_2$, y $T$.
2. Usando la derivada de $I(\lambda_1 , \lambda_2)$ con respecto $T$ demuestre que, para una temperatura dada, hay un intervalo de longitudes de onda en el cual $I(\lambda_1 , \lambda_2)$ es una función lineal de $T^{-1}$ e indique cuál es este intervalo.

3. Si $\lambda_1$ y $\lambda_2$ corresponden a los filtros $B$ y $V$ del sistema $UBV$ ( $\lambda_1 \sim 4500$Å, $\lambda_2 \sim 5500$Å) y $T \sim 5000$K, indique cual es la precisión que debe obtenerse en $I(B,V)$ para poder medir temperaturas con una incerteza menor que 100 K.