Let ![]() be the measured flux of a source unresolved with a beam having FWHM
of
be the measured flux of a source unresolved with a beam having FWHM
of ![]() and
and ![]() . The birghtness of the source is given by:
. The birghtness of the source is given by:
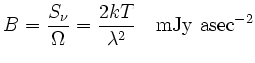 |
(3.1) |
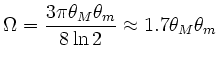 |
(3.2) |
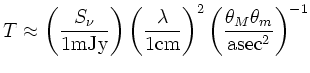 |
(3.3) |
Note that this is only a lower limit because the source can be much smaller than the beam implying a higher brightness.