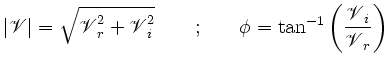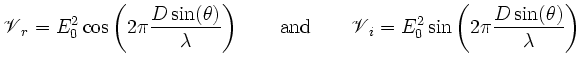

Next: Simple useful calculations
Up: Astronomy notes
Previous: AGN and Starburst Galaxies
Subsections
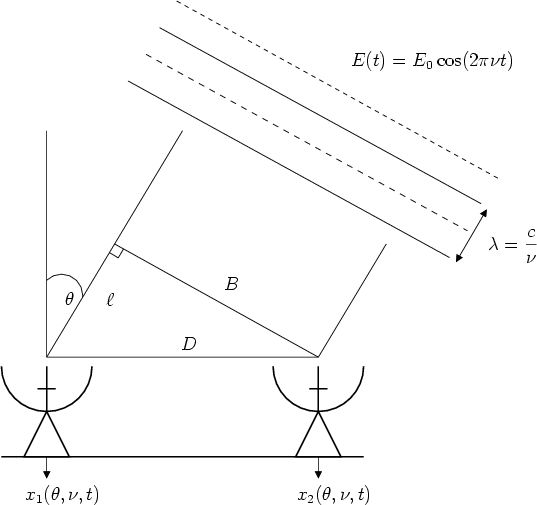
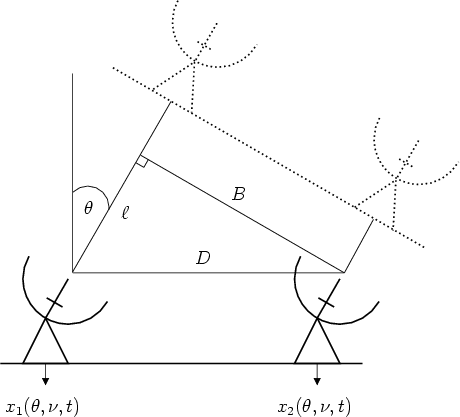
Figure 2.1:
General geometry of a single baseline interferometer.
 |
A radio interferometer is a set of two or more antennas collectively used to
measure the interference pattern produced by the angular brightness distribution
of a very distant source at a given frequency. The vector connecting any pair of
anntenas is called a baseline; its length defines the angular separation between
regions of constructive and destructive interference and consequently, the
resolution of the instrument. The geometry of a single baseline interferometer
is depicted in Figure 2.1. Two identical antennas are
separated by a distance 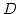 . An incident monochromatic plane wavefront
. An incident monochromatic plane wavefront 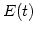 ,
radiated by a distant point source located at an angle
,
radiated by a distant point source located at an angle 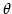 with respect to
the normal of the baseline, will arrive at the leftmost antenna with a time
delay of
with respect to
the normal of the baseline, will arrive at the leftmost antenna with a time
delay of
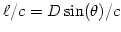 , or equivalently, with a phase difference of
, or equivalently, with a phase difference of
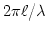 . Let
. Let 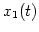 and
and 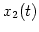 be the electric signals induced at
the output of each antenna. If the signals are combined according to the scheme
described on Figure 2.2, then the normalized system output is
given by:
be the electric signals induced at
the output of each antenna. If the signals are combined according to the scheme
described on Figure 2.2, then the normalized system output is
given by:
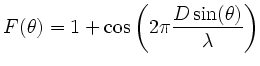 |
(2.1) |
This expression is known as the Total power interferometer response
function. Figure 2.3 presents a record of the transit of two
"radio stars" obtained using this principle [Ryle et al., 1950]. Note that the
interferometer used for this observations is a non-tracking interferometer which
means that the antennas are not steered towards the source but instead they
remain at a fixed position.
Figure 2.2:
Left: Total power interferometer. Right: Top: Response function (equation
2.1) using a value of
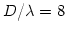 . Bottom: The same as before
but considering the directivity
. Bottom: The same as before
but considering the directivity 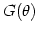 of the antennas assumed to be
circular apertures with
of the antennas assumed to be
circular apertures with
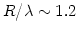 . Compare with the observations of
real point sources shown in figure
2.3
. Compare with the observations of
real point sources shown in figure
2.3
![\begin{picture}(4.5,7.15)(0,0)
\put(0,7.15){\makebox(0,0)[b]{$x_1(\theta,\nu,t)$...
....25){\vector(0,-1){1}}
\put(1.85,0){\makebox(0,0)[l]{$F(\theta)$}}
\end{picture}](img73.png)
![\includegraphics[width=0.5\columnwidth]{FIGURES/response.ps}](img74.png) |
Figure 2.3:
Record obtained using an east west total power interferometer. The
sources are Cygnus A (16:20) and Cassiopeia A (19:30). (Taken form
Ryle et al. [1950]). Compare with the total power interferometer response shown in
figure 2.2.
|
|
A more complex configuration known as multiplying interferometer is shown
in figure 2.4. We see three major differences when compared with
the previous one. First, an instrumental delay of
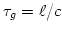 has been
included to compensate the geometrical delay, in other words, the phase center
has been displaced to the direction
has been
included to compensate the geometrical delay, in other words, the phase center
has been displaced to the direction 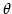 . Second, the antennas have been
steered to the same direction. The interplay between delay and steering produces
an "equivalent" interferometer whith a baseline of length
. Second, the antennas have been
steered to the same direction. The interplay between delay and steering produces
an "equivalent" interferometer whith a baseline of length
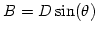 as
shown in figure 2.5. Finally, both signals have been split in two
branches to form the in-phase and quadrature products. Both outputs are then
combined in a single expression using complex notation:
as
shown in figure 2.5. Finally, both signals have been split in two
branches to form the in-phase and quadrature products. Both outputs are then
combined in a single expression using complex notation:
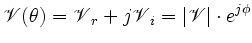 |
(2.2) |
where
with
Figure 2.4:
Multiplying interferometer.
![\begin{figure}\centering %%
\begin{picture}(6.65,10.15)(0,0)
\put(0.15,10.15){\m...
...9){\makebox(0,0)[l]{$x_2(\theta,\nu,t+\tau_g)$}}
\end{picture}\hfil \end{figure}](img81.png) |
Figure 2.5:
General geometry of a single baseline tracking interferometer. The
equivalent interferometer with an antenna separation of 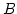 is shown in dotted
lines (see the text for details).
is shown in dotted
lines (see the text for details).
 |


Next: Simple useful calculations
Up: Astronomy notes
Previous: AGN and Starburst Galaxies
Rodrigo Parra
2005-07-15

![]() . An incident monochromatic plane wavefront
. An incident monochromatic plane wavefront ![]() ,
radiated by a distant point source located at an angle
,
radiated by a distant point source located at an angle ![]() with respect to
the normal of the baseline, will arrive at the leftmost antenna with a time
delay of
with respect to
the normal of the baseline, will arrive at the leftmost antenna with a time
delay of
![]() , or equivalently, with a phase difference of
, or equivalently, with a phase difference of
![]() . Let
. Let ![]() and
and ![]() be the electric signals induced at
the output of each antenna. If the signals are combined according to the scheme
described on Figure 2.2, then the normalized system output is
given by:
be the electric signals induced at
the output of each antenna. If the signals are combined according to the scheme
described on Figure 2.2, then the normalized system output is
given by:
![\begin{picture}(4.5,7.15)(0,0)
\put(0,7.15){\makebox(0,0)[b]{$x_1(\theta,\nu,t)$...
....25){\vector(0,-1){1}}
\put(1.85,0){\makebox(0,0)[l]{$F(\theta)$}}
\end{picture}](img73.png)
![\includegraphics[width=0.5\columnwidth]{FIGURES/response.ps}](img74.png)
![\includegraphics[width=0.9\columnwidth]{FIGURES/ryle_fringes_1952.ps}](img75.png)